谈永光1,李荣建1,张媛1,刘军定1,王亚林1
(1. 西安理工大学 岩土工程研究所,西安 710048)
摘 要:桩基础的扩孔效应会对黄土的结构性弱化产生重要影响,并可能影响和改变桩-土之间的相互作用。针对在结构性黄土地区的桩基础,本文首先基于小孔扩张理论分析了单桩扩孔条件下桩周土体的广义剪应变、广义剪应力的关系;然后,本文通过三轴试验得到了不同应力水平条件下的广义剪应力和应变关系;最后,将黄土结构性参数引入到单桩扩孔的分析中,研究了扩孔效应导致的黄土结构性参数的衰减变化规律。研究表明:在单桩扩孔效应作用下,距离桩轴越近,黄土的结构性参数衰减越剧烈,桩周黄土的结构性参数衰减到1.0;距离桩轴越远,黄土的结构性参数衰减越小,且在无限远处黄土的结构性参数接近原状黄土的初始结构性参数。
关 键 词:单桩;扩孔效应;结构性黄土;结构性参数;衰减
1 引言
在我国黄土地区桩基工程在建筑工程、高速公路和铁路应用越来越多,而黄土的结构性直接影响着黄土的力学性质以及桩-土之间的相互关系。因此,对于在黄土中研究桩基扩孔问题中,由于扩孔效应导致黄土地基中黄土的结构性衰减规律是一个亟待解决的工程问题之一。
在黄土的结构性的研究方面,目前国内许多学者对黄土的结构性进行过深入的研究,比较有代表性的成果有应变结构性参数[1],原状黄土结构性定量化参数[2]、应力比结构性参数 [3] 。基于应力比结构性参数,李荣建等提出了初始结构性参数和加载结构性参数,并将这些结构性参数引入到结构性黄土边坡的稳定性分析中,研究了结构性参数分布与边坡失稳之间的规律[4]。然而,在桩基础打桩问题中,至今还没有相应的研究开展打桩扩孔效应对黄土结构性的影响。因此,有必要将黄土结构性参数引入到桩基础打桩过程中并对黄土地基进行合理地评价。
在研究桩基础打桩沉桩的研究方面,小孔扩张理论作为一个理论分析方法起着重要的作用[5],Ladanyi研究了饱和粘土地基中小孔扩孔的理论解析解[6],Collins and Yu 等研究了地基中土体达到临界状态时不排水小孔扩孔的解析解[7],Davis and et al研究了速率效应的小孔扩孔的问题[8],周月健研究了土体内小孔扩张及挤土桩沉桩机理研究[9],周炳勤研究了小孔扩张理论及其工程应用[10],这些研究大都基于小孔扩张理论分析得出了不同条件下的桩周土的应力场、位移场等。这些研究大大推进了桩基础沉桩扩孔的相关研究,但对沉桩过程中结构性黄土地基因为打桩而受到扰动的分析还没有涉及,至今还没有相应的研究开展结构性黄土地基中打桩扩孔的影响效应评价,还没有涉及到结构性黄土的结构性参数变化规律的问题。因此,在黄土地基中开展研究沉桩扩孔对黄土结构性参数的影响规律具有重要的理论意义。
本文首先基于小孔扩张理论分析了单桩扩孔条件下桩周土体的广义剪应力、广义剪应变关系;然后,本文通过三轴试验得到了不同应力水平条件下的广义剪应力和剪应变关系;最后,将黄土结构性参数引入到单桩扩孔的分析中,研究了扩孔效应导致的黄土结构性参数的衰减变化规律。最后通过算例,针对陕西西安南郊试桩工程,在Q3黄土层下进行了单桩扩孔分析,研究单桩扩孔效应对黄土结构性参数的影响规律。
2单桩扩孔中土体的广义剪应力、应变
将桩基础沉桩的过程可以看成是在不排水条件下,在无限土体中,扩张成一个与桩径相同的圆柱型小孔的过程,如图1所示。

图1 柱形小孔扩张剖面
为研究此类沉桩问题,需作出如下假定:
(1)小孔扩张前,土体具有各向等同性;
(2)土是均匀的、各向同性的理想弹性体;
(3)土体满足摩尔-库伦强度准则。
所以研究在无限土体中扩张出一个桩径为a的小孔时,在小孔的周围必然会形成一个应力影响区,如图2所示。图中符号:R为应力影响范围,a为小孔的扩张半径(即桩径)。
图2柱形小孔扩张的平面图
由于无限长小孔扩张是轴对称课题,所以竖向、切向和径向应力都是主应力,现在距桩轴距离r的位置,取一个单元体进行分析,如图3所示.。图中符号:σz 为土单元的竖向应力;
σr为土单元的径向应力;
σθ为土单元的切向应力;
dz 为土单元的埋置深度;
r 为土单元距桩轴的距离。
图3 轴对称条件下土单元的应力状态
在小孔扩张这一轴对称条件下,存在广义剪应力与广义剪应变存在如下关系:
式中:
q为广义剪应力
εs为广义剪应变
εz 为竖向应变
εr为径向应变
εθ为切向应变
同时,假定不排水三轴试验广义剪应力—广义剪应变可由下列方程近似表示:
其中,D为曲线拟合参数,qult为极限剪应力。
基于以上条件和假设,Collions and Yu[7]推导了从零半径开始单桩扩孔的问题中,认为广义剪应力和广义剪应变都为a/r的函数,得到了广义剪应变可以表示为:
将上式(4)代入公式(3),可以来确定单桩扩孔后桩周土体的广义剪应力场分布:
由此单桩扩孔中桩周土体的广义剪应力、剪应变为引入黄土结构性参数奠定了理论基础。
3单桩扩孔中黄土结构性参数的引入
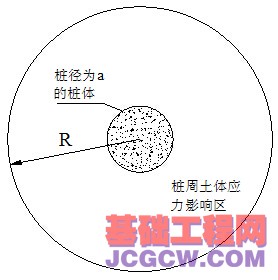
为了分析单桩扩孔中黄土结构性的变化规律,针对陕西西安南郊某试桩工程场地Q3黄土地层,本研究通过固结不排水常规三轴试验得到原状黄土的广义剪应力q与广义剪应变εs关系曲线(图4),可以从曲线上确定的极限剪应力qult,结合公式(3)进行拟合,从而得到不同围压条件下的曲线拟合参数D。
图4在15%含水量下原状黄土广义剪应力与剪应变
根据固结不排水三轴试验结果,可以得出50kPa、100kPa、200kPa围压下qult分别为480kPa、622kPa、730kPa,各围压条件下相应的拟合参数D分别为0.3836、0.9225、1.3425。 不同围压条件下的广义剪应力公式(3)即可表达为:
在50kPa围压下
在100kPa围压下
在200kPa围压下
目前,针对已经提出的结构性参数有应力比结构性参数mη,并分为指数形式的应力比结构性参数和对数形式的应力比结构性参数[3]。但是将这两种结构性参数描述方法作为客观规律应用于有限元分析时会给计算带来许多困难。因此,李荣建等将结构性参数的描述方法进行了改进[4],得到初始结构性参数的公式(9)和加载扰动结构性参数的公式(10),其中Q3黄土土体试验拟合参数H为2..0。
式中
mη加载过程结构性参数;
mη0为加载初始结构性参数;
为初始含水率;
σ2为初始围压;
εs为广义剪应变。
为了研究桩基础的扩孔效应对黄土的结构性弱化产生的影响,本研究将从零半径开始单桩扩孔的问题中广义剪应变表示式(公式(4))代入公式(10)中,同时将公式(9)亦代入公式(10)中,可以得到单桩扩孔后桩周黄土的结构性参数的计算公式为:
4扩孔中结构性参数的衰减分析
4.1黄土地基试桩工程概况
针对陕西西安南郊试桩工程,场地Q3黄土层厚约23米左右,工程试桩采用预应力管桩,试桩桩长为15米,管桩直径为500mm。本研究取土深度约3.5米~4.5米,经过室内常规实验测定,该黄土的天然含水率为15%,天然密度为2.0g/cm3,干密度为1.54g/cm3。
本研究选择分析埋深2.5m、5m及10m处黄土体的剪应力场和结构性参数场的变化规律(如图5所示)。
图5 单桩扩孔试桩剖面
4.2不同埋深下黄土的广义剪应力分布
本试桩工程的工程桩的桩径为500mm,即桩半径为250mm,根据小孔扩张后的广义剪应变公式(4),广义剪应变可以表示为:
另一方面,在2.5m、5m以及10m埋深处土层的自重应力分别为50kPa、100kPa以及200kPa。结合本研究中试验确定的土体广义剪应力、广义剪应变拟合参数D,将广义剪应变公式(12)代入公式(6)、(7)和(8),可以确定不同深度处的土体广义剪应力为:
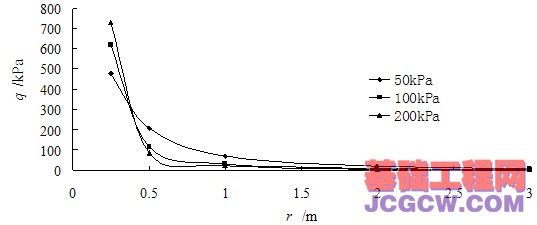
在桩周土体广义剪应力的表达式中,广义剪应力q为距桩轴距离r的函数式,为研究其变化规律,可以取不同桩轴距离r值进行计算,根据计算结果可以得到广义剪应力随桩轴距离r的分布曲线,如下图所示:
图6 广义剪应力q沿桩径方向的的衰减
从图6中广义剪应力变化趋势可以看出,当埋深一定时,由于单桩扩孔引起的广义剪应力
q随着距桩轴距离r的增大而呈现衰减趋势,最终趋近于零;当
r值一定时,
q随深度的增大也呈现衰减趋势。
4.3不同埋深下黄土结构性参数变化规律
通过室内试验得到结构性黄土的天然含水量
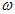
、不同埋深下初始应力
σ2代入公式(9)可以得出初始结构性参数
mη0的值,在2.5m、5m以及10m埋深处初始结构性参数
mη0分别为11.8063、11.1378和9.8008。通过初始结构性参数分布可知,地基顶部土体的初始结构性参数最大,初始结构性参数从地基顶部向下逐渐减小,主要原因是地基深部应力值大于地基上部的应力值。
通过公式(12)计算得出广义剪应变
εs,然后将广义剪应变
εs代入公式(11),可以得到不同埋深下的加载结构性参数
mη的值(详见公式(16)、(17)、(18)):
当埋深为2.5m时:
由式(16)可以看出,结构性参数mη随着r的减小而呈现非线性的衰减;距离桩轴越近,黄土的结构性参数衰减越剧烈,衰减到最小值为1.0;距离桩轴越远,黄土的结构性参数衰减越小;当r接近于无穷远处,可以计算出mη=11.8063,与式(9)计算得到的初始结构性参数mη0=11.8063一致。黄土结构性参数mη与距桩轴距离r的关系,如图7所示。
图7地基深度2.5m时结构性参数的衰减规律
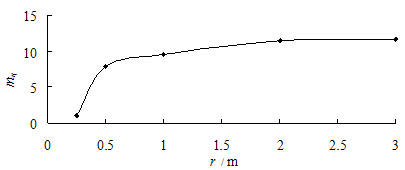
当埋深为5m时:
由式(17)可以看出,结构性参数mη随着r的减小而呈现非线性的衰减,衰减到最小值为1.0。当r接近于无穷远处,可以计算出mη=11.1378,与式(9)计算得到的初始结构性参数mη0=11.1378完全一致。黄土结构性参数mη与距桩轴距离r的关系,如图8所示。
图8地基深度5m时结构性参数的衰减规律
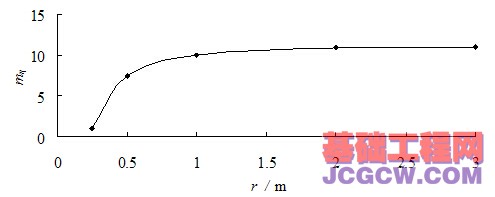
当埋深为10m时:
由式(18)可以看出,结构性参数mη随着r的减小而呈现非线性的衰减,衰减到最小值为1.0。当r接近于无穷远处,可以计算求得mη=9.8008,与式(9)计算得到的初始结构性参数mη0=9.8008完全一致。黄土结构性参数mη与距桩轴距离r的关系,如图9所示。
图9地基深度10m时结构性参数的衰减规律
根据计算得到的在不同埋深时黄土体的结构性参数表达式中,取r=0.5m,可以得到距桩轴相同距离条件下结构性参数mη随地基深度z的变化规律(如图10所示)。图中可以看出,当r=0.5m时,结构性参数mη随地基深度Z大致呈线性衰减。
图10土体结构性参数随深度的变化规律
总之,通过对比分析表明,(1)当地基深度一定时,结构性参数mη随着r的减小而呈现非线性的衰减;距离桩轴越近,黄土的结构性参数衰减越剧烈;距离桩轴越远,黄土的结构性参数衰减越小;无限远处的结构性参数接近原状黄土的初始结构性参数。(2)距桩轴相同距离条件下,结构性参数mη随地基深度z大致呈线性衰减。
5 结论
(1)基于小孔扩张理论分析了单孔扩张后的桩周土体的广义剪应力和广义剪应变表达式,并且引入黄土的结构性参数,为单孔扩张后桩周黄土体结构性参数变化分析奠定了理论分析基础。
(2)基于三轴试验得到的不同应力水平条件下的广义剪应力和广义剪应变关系,通过单桩扩孔计算和分析,得到了广义剪应力和距桩轴距离、埋置深度的关系:当埋置深度一定,桩周土体的广义剪应力随着距桩轴距离的增大而呈现衰减趋势,当距桩轴较近时,广义剪应力衰减较为剧烈,当距离桩轴较远时,广义剪应力的变化较为稳定,并在无限远处趋向于零;当距桩轴距离一定时,广义剪应力随埋置深度增加而大致呈现线性衰减趋势。
(3)通过研究单桩扩孔效应对黄土结构性参数的影响规律可知:随着黄土和桩轴的距离减小,结构性参数而呈现非线性的衰减;距离桩轴越近,黄土的结构性参数衰减越剧烈,衰减到最小值为1.0;距离桩轴越远,黄土的结构性参数衰减越小;无限远处的结构性参数接近原状黄土的初始结构性参数。
(4)单桩扩孔效应作用下,距桩轴相同距离时地基黄土的结构性参数随地基深度增大呈现大致的线性衰减。
参考文献
[1] 谢定义,齐吉林.土的结构性及其定量化参数研究的新途径[J].岩土工程学报,1999,21(6): 651-656.
XIE Ding-yi, QI Ji-lin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 1999,21(6): 651–656.(in Chinese)
[2] 邵生俊,周飞飞,龙吉勇.原状黄土结构性及其定量化参数研究[J].岩土工程学报,2004,26(7): 531-536.
SHAO Sheng-jun, ZHOU Fei-fei, LONG Ji-yong. Structural properties of loess and its quantitative parameter [J]. Chinese Journal of Geotechnical Engineering, 2004,26(7): 531-536.
[3] 邓国华, 邵生俊, 陈昌禄, 佘芳涛. 一个可考虑球应力和剪应力共同作用的结构性参数. 岩土力学, 2012, 33(8): 2310-2314.
DENG Guo-hua, SHAO Sheng-jun, CHEN Chang-lu,SHE Fang-tao A structural parameter reflecting coupling action between shear stress and spherical stress[J]. Rock and Soil Mechanics, 2012, 33(8): 2310-2314.
[4] 李荣建,郑文,刘军定,闫蕊,邵生俊.考虑初始结构性参数的结构性黄土边坡稳定性评价[J].岩土力学,2014,35(1):143-150.
LI Rong-jian, ZHENG Wen, LIU Jun-ding, YAN Rui, SHAO Sheng-jun. evaluation of stability of structural loess slope considering initial structural parameters[J]. Rock and Soil Mechanics, 2014,35(1): 143-150.
[5] 余海岁.岩土介质小孔扩张理论[M].北京:科学出版社,2013: 26-69.
Hai-Sui Yu. Cavity Expansion Methods in Geomechanics[M]. BeiJing: Science Press, 2013:26-69.
[6] Ladanyi, B. Expansion of a cavity in a saturated clay medium.Journal of the Soil Mechanics and Foundations Division, ASCE, 1963, 89(SM4):127-161.
[7] Collins, I.F. and Yu, H.S. Undrained expansions of cavities in critical state soils. International Journal for Numerical and Analytical Methods in Geomechanics, 1996,20(7): 489-516.
[8] Davis,R.D., Scott,R.F.and Mullenger,G. Rapid expansion of a cylindrical cavity in a rate-type soil. International Journal for Numerical and Analytical methods in Geomechanics, 1984, 8(2):125-140.
[9] 周月健.体内小孔扩张及挤土桩沉桩机理研究[D].浙江:浙江大学,2001.
ZHOU Yue-jian. A Study on spheric cavity expansion and static piling in soils[D]. Zhejiang: Zhejiang University.
[10] 周炳勤.小孔扩张理论及其应用[D].南京:东南大学,2005.
ZHOU Bing-qin. The Theory Of Spherical Cavity Expansion and Its Application[D]. Nanjing: Southeast University, 2005.







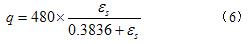


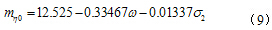

 为初始含水率;σ2为初始围压;εs为广义剪应变。
为初始含水率;σ2为初始围压;εs为广义剪应变。





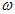 、不同埋深下初始应力σ2代入公式(9)可以得出初始结构性参数mη0的值,在2.5m、5m以及10m埋深处初始结构性参数mη0分别为11.8063、11.1378和9.8008。通过初始结构性参数分布可知,地基顶部土体的初始结构性参数最大,初始结构性参数从地基顶部向下逐渐减小,主要原因是地基深部应力值大于地基上部的应力值。
、不同埋深下初始应力σ2代入公式(9)可以得出初始结构性参数mη0的值,在2.5m、5m以及10m埋深处初始结构性参数mη0分别为11.8063、11.1378和9.8008。通过初始结构性参数分布可知,地基顶部土体的初始结构性参数最大,初始结构性参数从地基顶部向下逐渐减小,主要原因是地基深部应力值大于地基上部的应力值。






 成功提示
成功提示 错误提示
错误提示 警告提示
警告提示
评论 (0)