2025-10-22 3490 0
用一种新的损伤塑性模型捕捉岩石的压力和速率相关行为
Capturing pressure- and rate-dependent behaviour of rocks using a new damage-plasticity model

摘要: 岩石对围压和应变率的响应可以从非常脆性转变为延展性。捕捉到这一转变对于准确预测采矿中爆破、爆炸或钻探引起的岩体破坏是至关重要的。在这项工作中,提出了一个新的本构模型,它考虑了围压和应变率对干燥完整岩石和其他类似地质材料的名义强度和峰后行为的影响。该本构模型的主要特点是采用了从初始屈服到最终破坏的单一加载函数和依赖于速率的增强,从而能够真实地描述不同围压下的应变率效应。该模型能够很好地反映材料的脆性和延性响应,以及应变速率和围压的脆韧转变过程。 引言: 了解和模拟岩石的行为将为岩土工程和采矿工程中的安全和经济设计铺平道路。与任何其他地质材料一样,岩石的行为取决于应变率和压力,也就是说,在极高的围压或高应变率下,岩石的响应可以从非常脆性变为延展性。在地壳岩层的采矿和岩土工程作业中,爆破、钻探或隧道开挖和/或构造和地震力的影响可以极大地改变应力状态。因此,对破坏的预测需要一个能够尽可能准确地捕捉到岩石在相当复杂的应力状态和不同加载速率下的宏观响应的模型。 岩石细观非弹性变形涉及一系列导致材料微结构退化的细观力学过程。这些过程通常开始于启动材料基质中的微裂纹(在低压下)和/或颗粒(在高压下),然后是具有一定厚度的带的微裂纹的局部化,在那里微裂纹最终结合形成宏观断裂。在整个非弹性变形过程中,微裂纹两面之间的摩擦滑动、粗糙度互锁、颗粒流和/或扩散流、晶体塑性以及其他过程都可能伴随着微裂纹和破裂。这些变形的微观机制是在宏观尺度上观察到的,如刚度和强度降低、非弹性膨胀/压实和残余应变。从现象学的角度来看,所有导致刚度和强度降低的机制都可以描述为损伤,而导致残余应变发生的所有现象都可以解释为塑性变形。此外,岩石变形的微观力学过程大多是时间/速率相关的,这就导致了宏观上观察到的岩石的速率相关行为。这种依赖时间/速率的微观机制的例子可以是静态摩擦的时间依赖、摩擦强度随加载速率的演变或依赖时间的微裂纹扩展。与速率相关的宏观岩石行为可以用岩石中的增加来表征高应变率下的拉伸和压缩强度。此外,在较高的应变率下,岩石表现出更具延性的倾向,而在准静态加载下,在相同的围压下,岩石的行为可能完全是脆性的。 已经提出了具有不同复杂程度和适用性的唯象损伤-塑性耦合模型来模拟岩石的力学行为。一般来说,这些模型在模型公式中指定了损伤和塑性过程之间的相互作用,以便同时考虑在非弹性变形过程中观察到的刚度和强度降低以及残余应变。建立岩石损伤-塑性耦合模型可以采用多种方法,以反映围压对岩石力学行为的影响。这种方法的例子可以是具有两个加载面的模型,或者其中损伤演化被定义为体积塑性应变率的函数的模型。尽管在文献中已经发现了许多能够描述不同围压下岩石力学行为的损伤-塑性耦合模型,但对于考虑围压和加载速率的综合影响,特别是对岩石的脆韧性转变的模型的建立,还没有引起太多的关注。 在这项研究中,通过采用组合屈服-破坏函数,发展了一种新的公式,它不需要多个加载面,同时便于模型的实施和应用,以涵盖不同压力和应变率下的广泛响应。在该公式中,初始屈服面随着定义为累积塑性应变率的函数的损伤变量的演化而演变为线性摩擦破坏包络。这是所提出的模型的一个重要特征,因为随着围压的增加,脆性/软化和延性/硬化响应以及两种行为状态之间的转变可以被模型自动捕捉,而不需要单独定义硬化或软化规律。通过模拟微裂纹闭合对岩石力学响应的影响,还解释了决定岩石从拉伸载荷转换为压缩载荷时的行为的基本机制。此外,在岩石和其他类似地质材料中实验观察到的行为的应变率相关性,通过Perzyna型粘度被纳入模型中。值得注意的是,所提出的模型中的速率依赖被视为模型的内在特征,而不是数值实现中的正则化技术。此外,在这项研究中还没有考虑潮湿岩石中孔压引起的速率相关响应,这是我们未来工作中需要解决的一个问题。在所提出的模型公式中,分离了压力和速率依赖关系,允许在准静态和动态加载条件下对模型进行独立校准。我们认为,这有利于模型的开发和校准。 本文首先描述了模型公式,并提供了模型公式与岩石在不同围压和应变率下的特性之间的联系。然后描述了数值实现算法,并给出了不同围压和应变率下岩石行为的数值例子,以展示新模型的良好特性。 图表
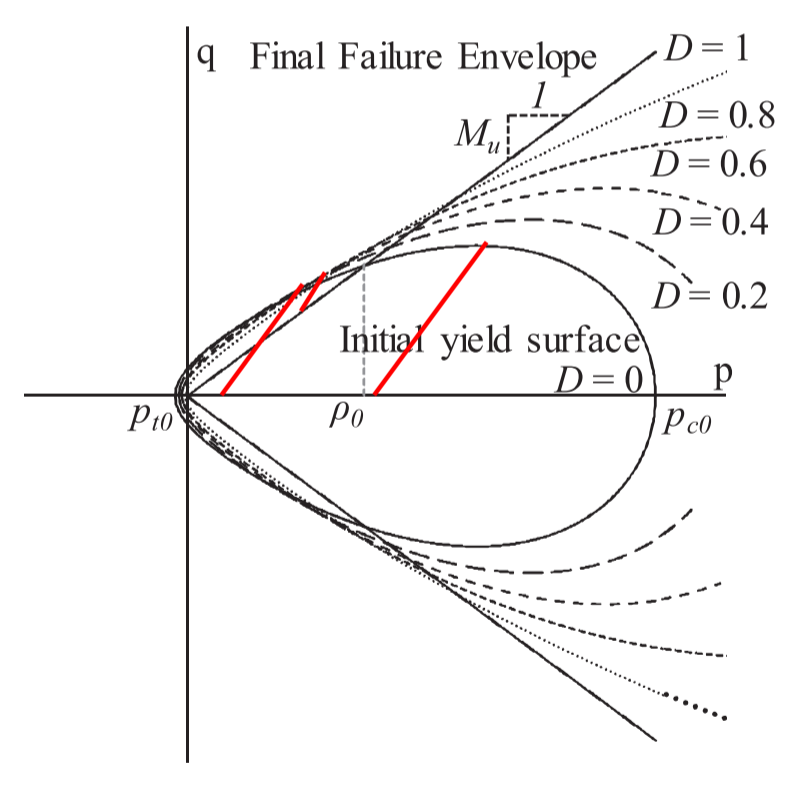
图1 应力空间中含损伤的屈服面演化

图2 二维应力返回算法的图解

图3 奥吉格花岗岩和戈斯福德砂岩的初始屈服面
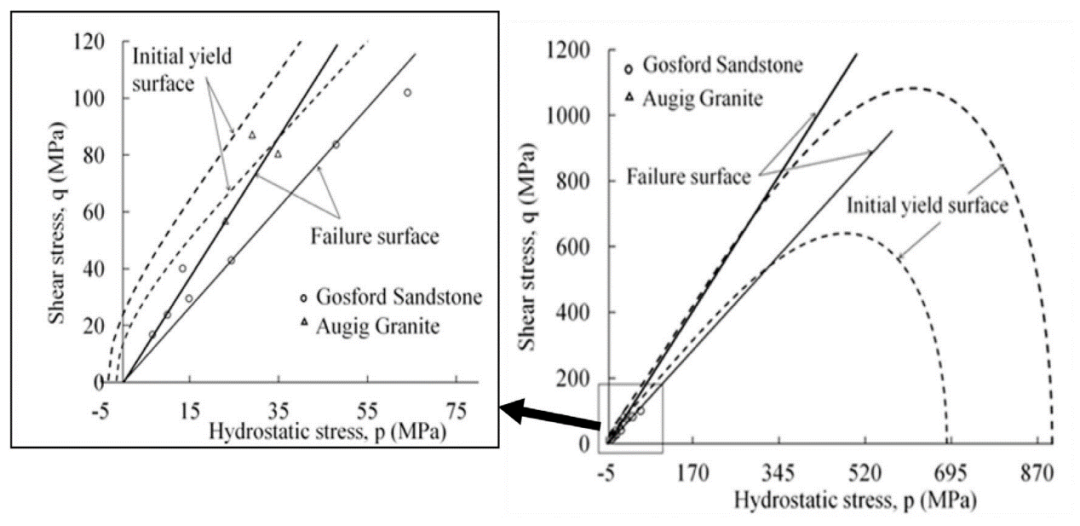
图4 奥吉格花岗岩和戈斯福德砂岩破裂面的标定
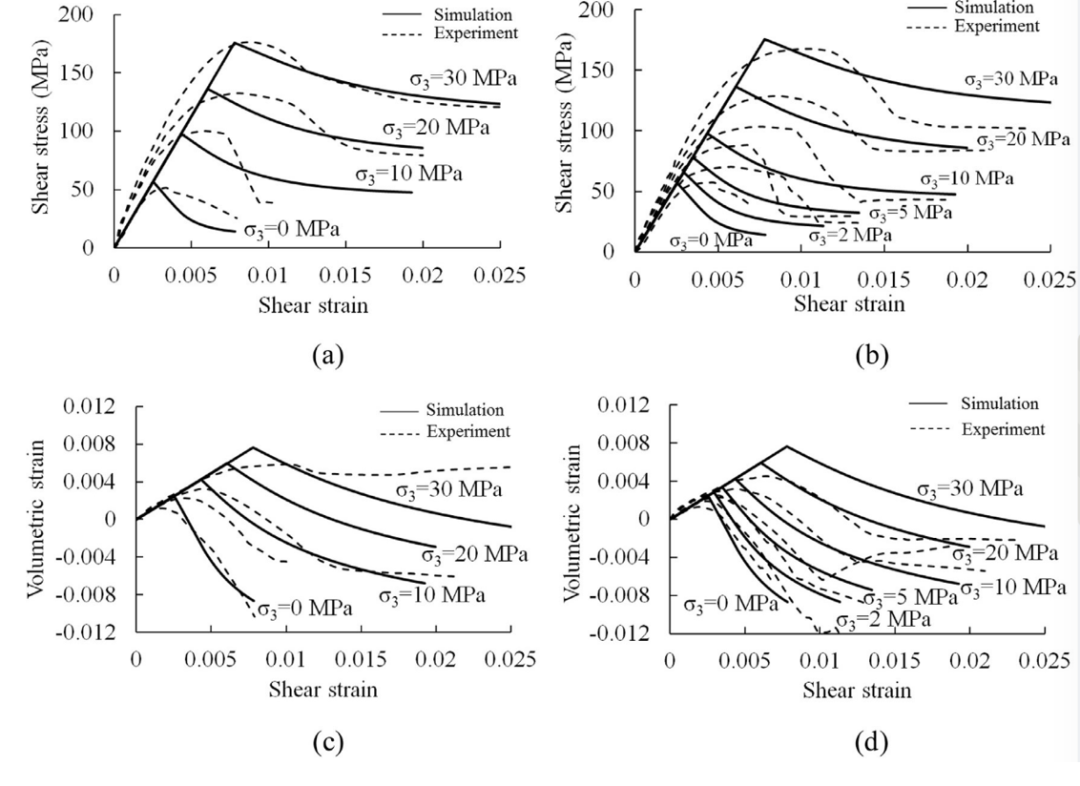
图5 戈斯福德砂岩在三轴压缩试验下的(a,b)应力-应变和(c,d)体积响应
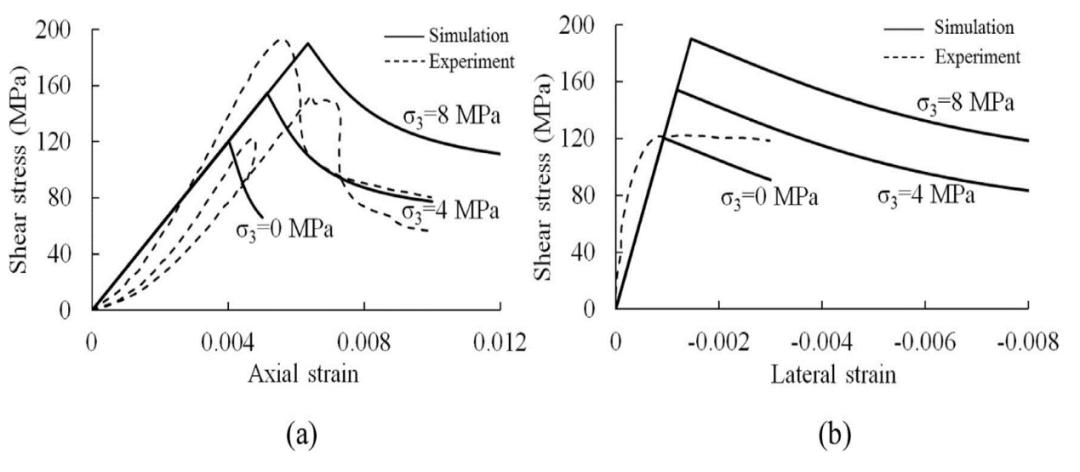
图6 奥吉格花岗岩在三轴压缩试验中对(a)轴向应变(b)侧向应变的剪应力响应
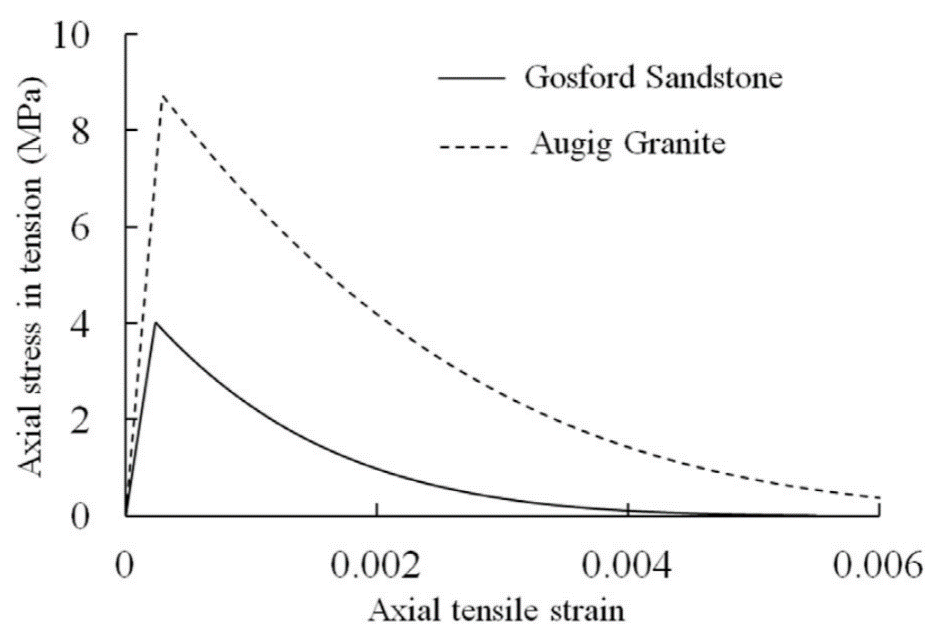
图7 奥吉格花岗岩和戈斯福德砂岩在单轴拉伸试验下的轴向应力-应变响应
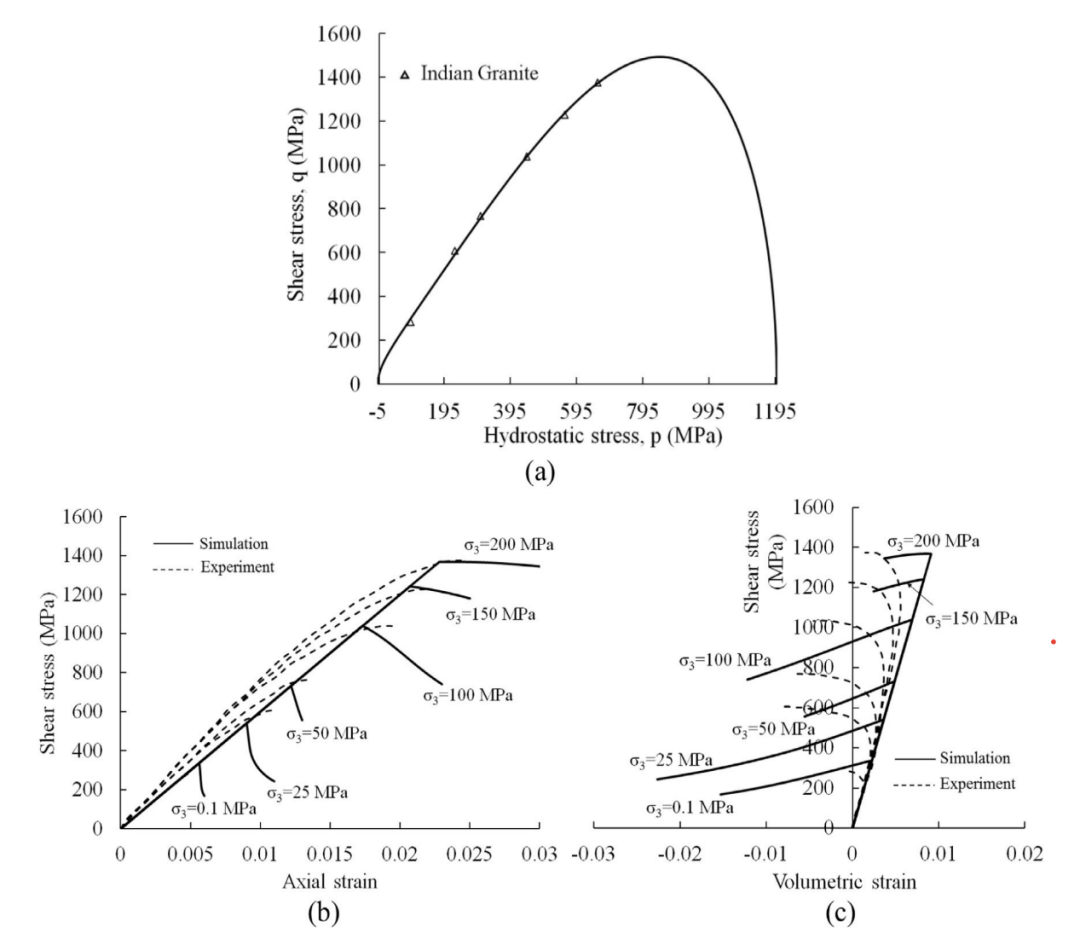
图8 印度花岗岩的速率无关特性的校准和预测(a)初始屈服面,(b)轴向应变-剪应力和(c)体积应变-剪应力响应
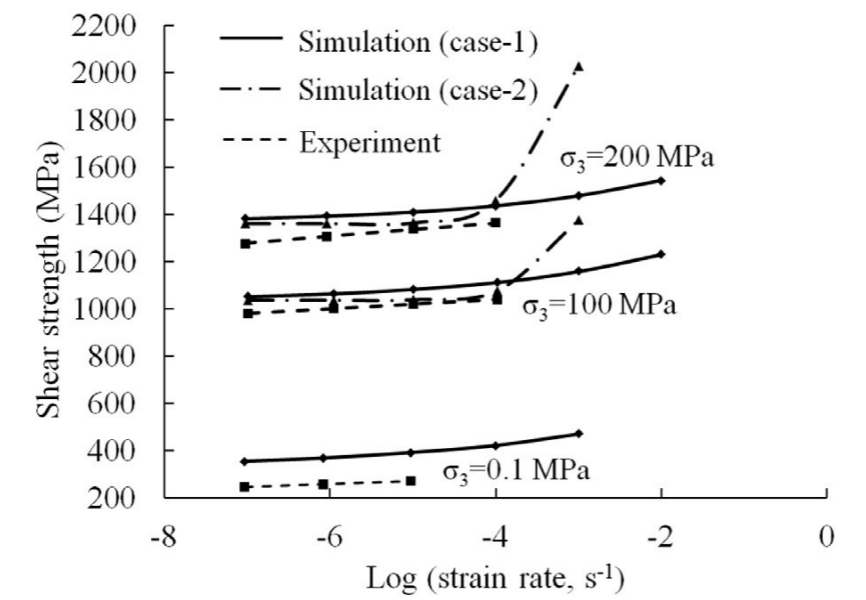
图9 三轴压缩下印度花岗岩在不同围压下的剪切强度随应变率的变化
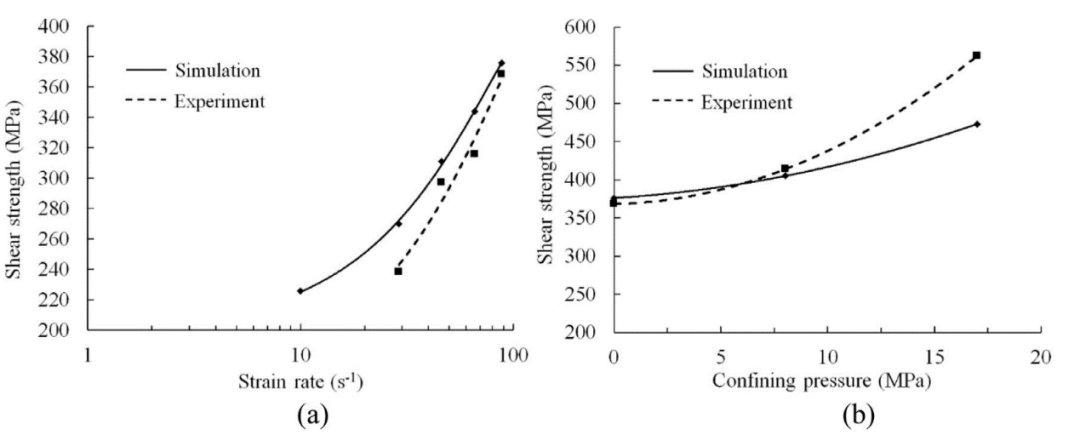
图10 花岗岩抗剪强度的变化--(a)不同应变率下的UCS预测和(b)不同应变率围压下的抗剪强度

图11 应变速率对印度花岗岩脆-韧性转变的影响
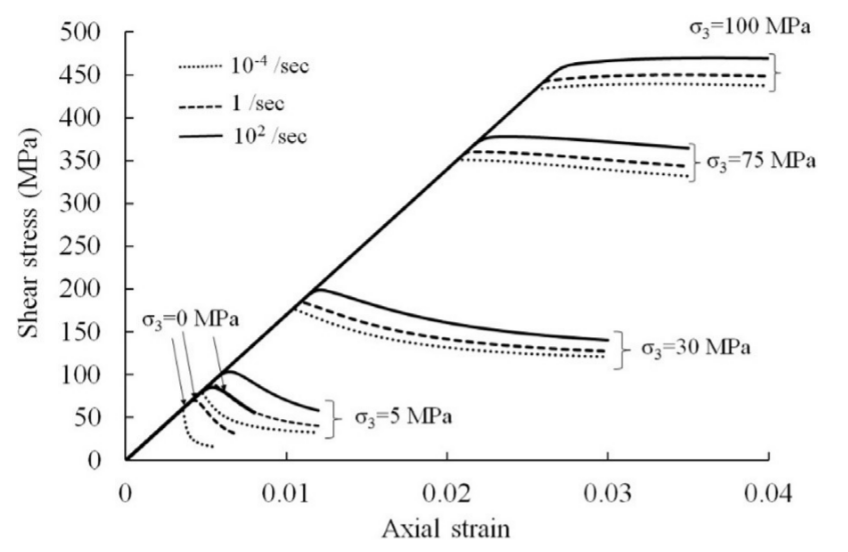
图12 约束和应变率对戈斯福德砂岩三轴压缩应力-应变特性的综合影响
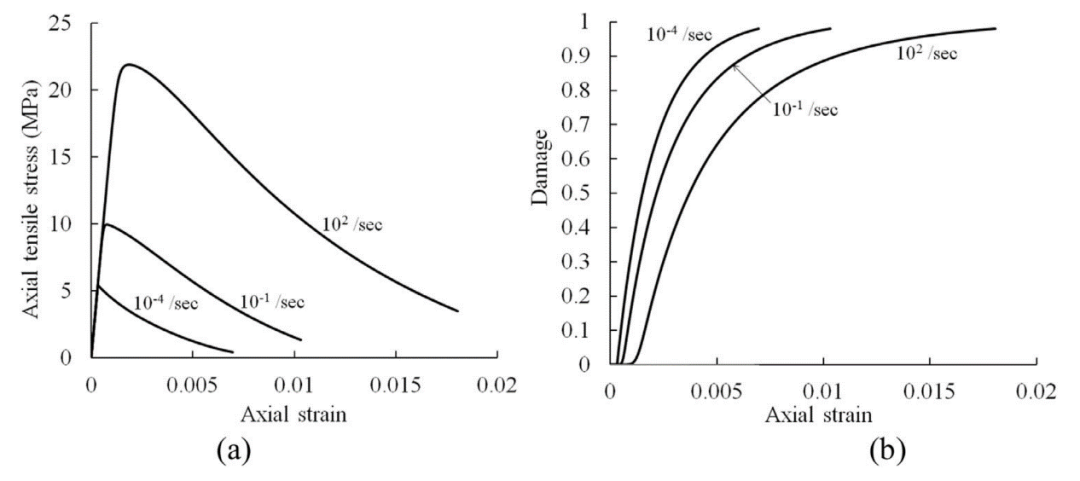
图13 应变率对(a)戈斯福德砂岩在单轴拉伸下的应力-应变响应(b)后续损伤演化的影响
结论: 我们提出了一个新的模型,同时考虑了围压和应变率对岩石特性的影响。所提出的模型简单而通用,足以捕捉到围压和应变率共同作用下的各种行为。它的演化屈服函数允许描述脆性和延性响应以及它们的转变,而不需要明确的软化/硬化定律,而依赖于速率的增强依赖于单一的粘度参数,并且对大范围的围压有效。实验测试表明,该模型在预测不同加载条件下岩石的复杂性态方面具有良好的特点。这对于分析采矿和资源工程中的大规模破坏是必不可少的。另一方面,目前的模型仍然需要改进,以考虑潮湿岩石中孔压引起的速率相关性。
Hot News
 成功提示
成功提示
 错误提示
错误提示
 警告提示
警告提示
评论 (0)